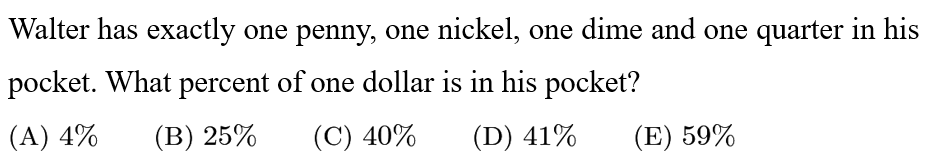
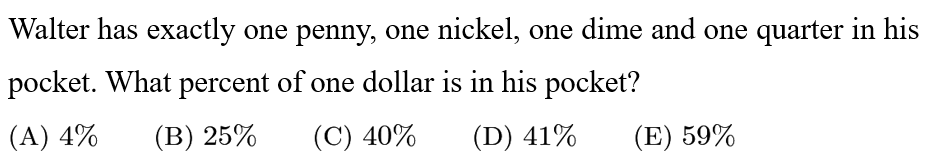
Answer: D
Solution:
Walter has 1+5+10+25=41 cents in his pocket. There are 100 cents in a dollar. Therefore, Walter has 41/100=41% of a dollar in his pocket.
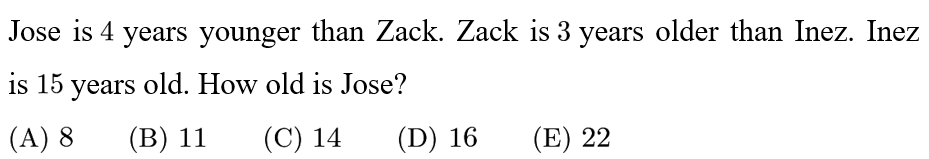
Answer: C
Solution:
Zack is 3 years older than Inez, who is 15. Therefore, Zack is 15+3=18 years old.
Jose is 4 years younger than Zack, who is 18. Therefore, Jose is 18-4=14 years old, and the answer is C.

Answer: E
Solution:
Dividing by 3/5 is the same as multiplying by its reciprocal, 5/3. Multiplying a number by two numbers is the same as multiplying the number by the product of those two numbers. Thus, multiplying by 3/4 and then 5/3 is the same as multiplying by 3/4*5/3=5/4. , and the answer is E.

Answer: C
Solution:
Ben adds 1 to 6, getting 7. Then Ben doubles it, to get 14. He gives this number to Sue. Then Sue subtracts 1 from the number, to get 13. Finally, Sue doubles the result to get 26, and the answer is C.
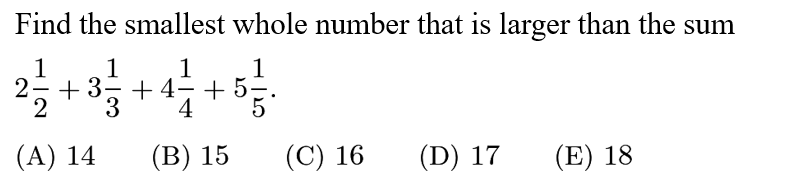
Answer: C
Solution:
Adding the whole numbers gives 2+3+4+5=14. Adding the fractions gives 1/2+1/3+1/4+1/5=30/60+20/60+15/60+12/60=77/60. This will create one more whole, and a fraction that is less than 1. Thus, the smallest whole number that is less than 15 plus some fractional part is 16, and the answer is C.
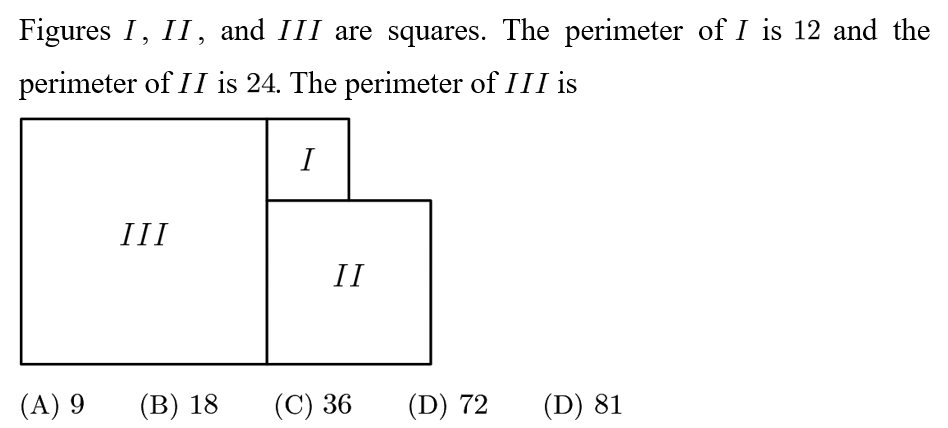
Answer: C
Solution:
Since the perimeter of I is 12, each side is 3.
Since the perimeter of II is 24, each side is 6.
The side of III is equal to the sum of the sides of I and II. Therefore, the side of III is 3+6=9.
Since III is also a square, it has an perimeter of 9*4=36, and the answer is C.

Answer: B
Solution:
The students who walk home are: 1-1/2-1/4-1/10=3/20.

Answer: D
Solution:
3000 lire/ 1.6dollars= x lire/ 1 dollar =>x=1875.
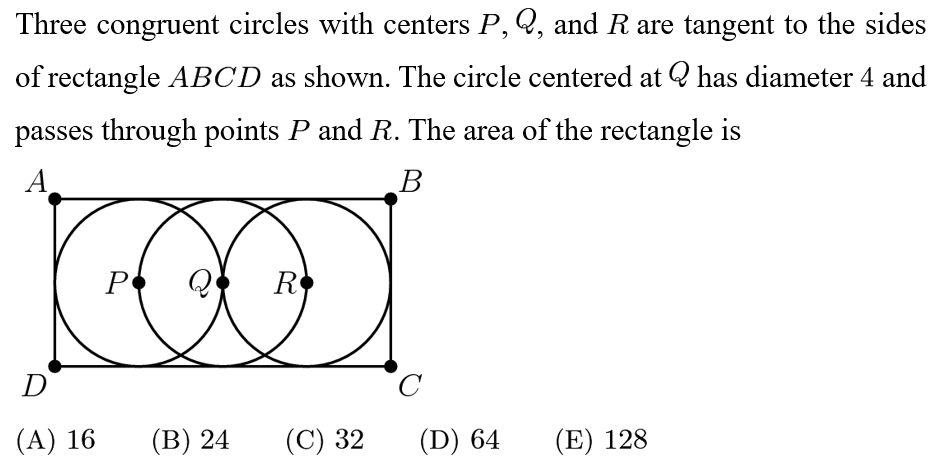
Answer: C
Solution:
If circle Q has diameter 4, then so do congruent circles P and R. Draw a diameter through P parallel to AD. The diameter will be congruent to AD, and thus AD=4, which is the height of the rectangle.
Draw a horizontal line PQR that extends to the sides of the rectangle. This line is 2 diameters long, so it has length 8. It is parallel and congruent to AB, so the width of the rectangle is 8.
Thus, the area of the rectangle is 4*8=32.

Answer: A
Solution:
Chris would have spent 40+80=120 dollars if there were no sale. The sale means that he saved 80*0.4+40*0.55=54 dollars. He saved54/120=45% off the total of the original prices.
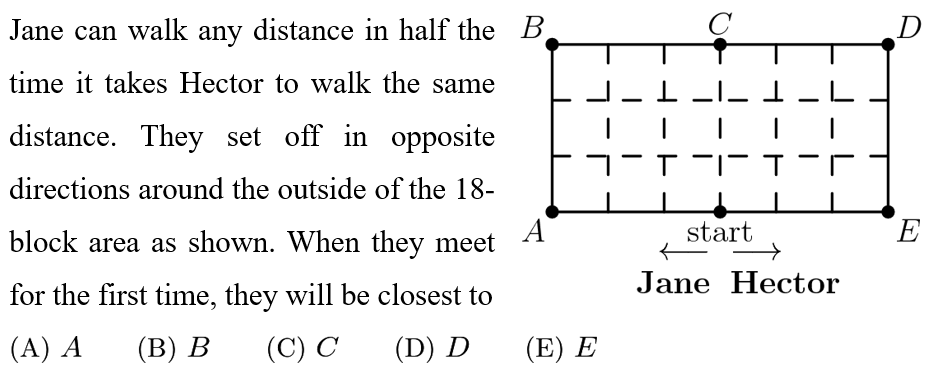
Answer: D
Solution:
Counting around, when Jane walks 12 steps, she will be at D. When Hector walks 6 steps, he will also be at D. Since Jane has walked twice as many steps as Hector, they will reach this spot at the same time. Thus, the answer is D.

Answer: E
Solution:
We examine only the factors of 90,91,92, 93, and 94 that are less than 13, because for a year to be lucky, it must have at least one factor between 1 and 12 to represent the month. 90 =9*10; 91=7*13; 92=4*23; 93=3*31; 94 has factors of 1 and 2. Dividing 94 by 2 gives 47, and no month has 47 days. Thus, 1994 is not a lucky year.
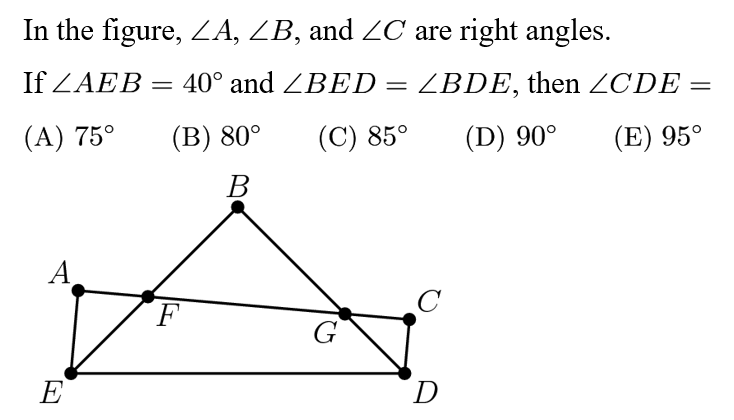
Answer: E
Solution:
Because <BED=<BDE, <B=90, we get<BED=<BDE=45. <AED=<AEB+<BED=40+45=85. Since ACDE is a quadrilateral, the sum of its angles is 360. Therefore: <A+<C+<AED+<CDE+360, =>90+90+85+<CDE=360, => <CDE=95.

Answer: B
Solution:
we can note that they will play a total of 50+40=90 games and must win 0.7*90=63 games. Since they won 40 games already they need 63-40=23 more games.

Answer: B
Solution:
4/37=0.108108108… Since this repeats every three digits, the 100th digit is 1.

Answer: C
Solution:
Altogether, the summer project totaled 7*3+4*5+5*9=86 days of work for a single student. This equals744/86=9 dollars per day per student. The students from Balboa school earned 9*4*5=180 dollars.

Answer: D
Solution:
By the tables, Annville has 11 6th graders and Cleona has 34. Together they have 45 6th graders and 300 total students, so the percent is 45/300=15%.

Answer: C
Solution:
The area taken up by the L's is 4*(3/16)=3/4 of the area of the whole square. What remains has 1/4 of the area of the larger square. 1/4* 100*100=50*50 is the area of the smaller square, so its side length is 50.
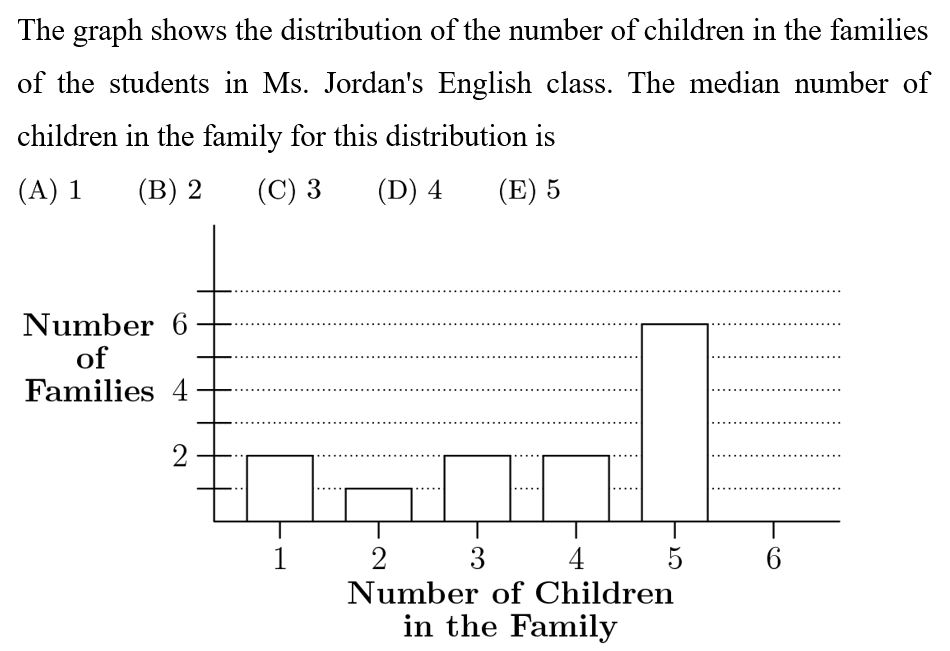
Answer: D
Solution:
Counting, there are thirteen total families. The middle number is 7th in either direction, and it is easy to see from the right side that this number is 4 .

Answer: B
Solution:
Note that the probability of Diana rolling a number larger than Apollo's is the same as the probability of Apollo's being more than Diana's. If we denote this common probability D, then 2D+P(Apollo=Diana)=1. Now all we need to do is find P(Apollo=Diana). There are 6*6=36 possibilities total, and 6 of those have Apollo=Diana, so P(Apollo=Diana)=6/36=1/6. Going back to our first equation and solving for D, we get 2D+1/6=1 =>D=5/12.
Method 2:
if Apollo’s number is 1, it is not possible large than Diana’s number;
if Apollo’s is 2, and Dianna’s is 1 then Apollo’s number is larger than Diana’s. the probability is 1/6*1/6=1/36;
if Apollo’s is 3, and Dianna’s is 1 or 2, then Apollo’s number is larger than Diana’s. the probability is 1/6*2/6=2/36;
if Apollo’s is 4, and Dianna’s is 1, 2 or 3, then Apollo’s number is larger than Diana’s. the probability is 1/6*3/6=3/36;
if Apollo’s is 5, and Dianna’s is 1, 2 3,or 4, then Apollo’s number is larger than Diana’s. the probability is 1/6*4/6=4/36;
if Apollo’s is 6, and Dianna’s is 1, 2 3,4,or 5, Apollo’s number is larger than Diana’s. the probability is 1/6*5/6=5/36;
Totally, the probability is 1/36+2/36+3/36+4/36+5/36=15/36=5/12.
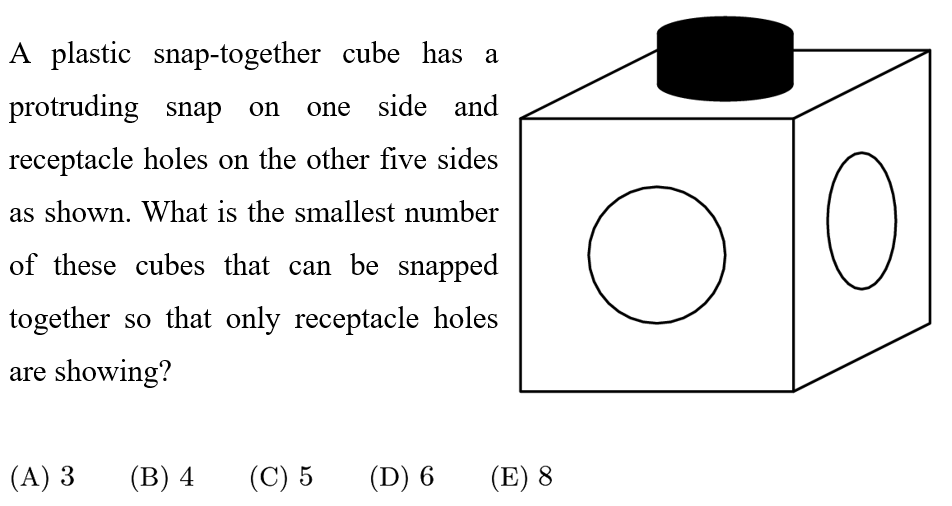
Answer: B
Solution:
It is rather easy to see that the only way that you can possibly have three cubes without protruding snaps is to have them in a triangle formation. However, in this case, the exterior angles are 120, whereas the outside angle of the cubes are 90 each. A square like formation will work in the case of 4 cubes, so the answer is B.

Answer: A
Solution:
The prime factorization of 6545 is 5*7*11*17, so every two-digit number pair has to be two number of the form pq. Now we do trial and error: 5*7=35, 11*17=185; (3 digit) ; 5*11=55, 7*17=119(3 digit) ; 5*17=85, 7*11=77(correct) , so 85+77=162.

Answer: B
Solution:
Count from left to right: There are 5 choices for the first digit, 5 choices for the second, 8 remaining choices for the third, and 7 remaining for the fourth, so there are 5*5*8*7=1400 numbers.
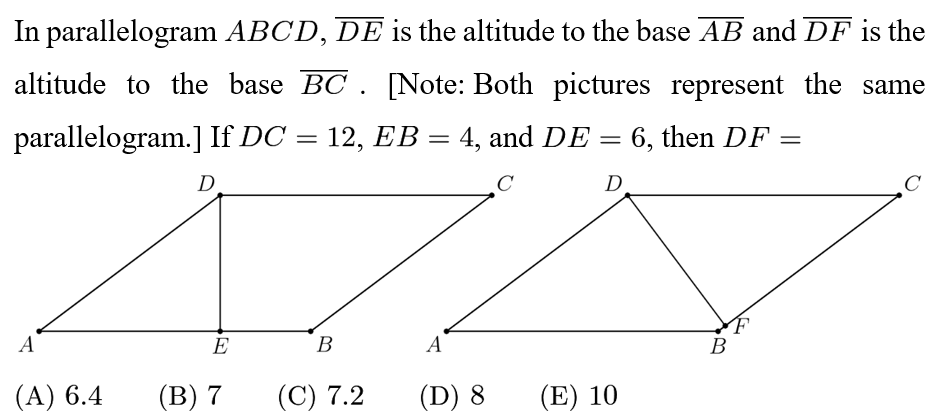
Answer: C
Solution:
Note that DE*AB=DF*BC=area(ABCD).
DE=6; AB=DC=12; so Area(ABCD)=6*12=72;
Since <DEA is a right angle, we can use the pythagorean theorem:AD=sqrt(AE*AE+DE*DE)=sqrt((AB-BE)^2+6*6)=sqrt((12-4)^2+6*6))=10;
BC=AD=10;
Now we can finally substitute: area(ABCD)=72=BC*DF=10*DF;=>DF=7.2.

Answer: D
Solution:
Say you are on the Houston-bound bus that left at 12:30, looking out the window to see how many buses you pass. At 12:45 pm, the Dallas bus that left at 8:00 am is 4:45 away from Dallas, Your bus is also 15 minutes from Houston. At 1:15 pm, the 9:00 am Dallas bus meets you again, being 45 minutes from Houston. you might notice that the buses meet you in 30 minute intervals after 12:45 pm; They are 12:45, 1:15, 1:45, 2:15, 2:45, 3:15, 3:45, 4:15, 4:45, 5:15, and 5:30, your arrival time.
AMC培训、答疑,请联系微信 / 电话:136 1118 1627
艾蕾特教育 @Elite Edu, 在这里,